난시 이해를 위한 광학, 그리고 교정 원리 – 2
안녕하세요 안과전문의 송한입니다.
난시 이해하기 세 번째 포스팅 입니다.
지난 포스팅에서는 정시, 원시 그리고 근시에 대해 간단히 알아보고 구면+원주 렌즈의 개념에 대해 알아보며 난시의 기본에 대해 살짝 알아보았습니다.
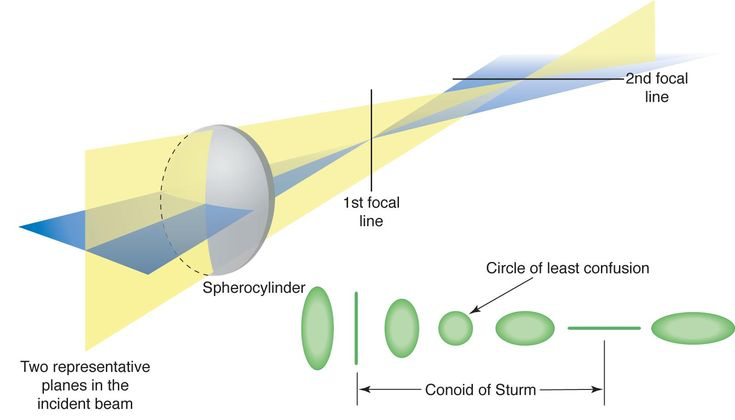
오늘 알아볼 내용은 Sturm of conoid 입니다.
차례
Sturm of Conoid
직역하면 “스텀의 원뿔”이란 이것은, 프랑스 안과의사 Jules Sturm이 만든 개념입니다.
난시(Astigmatism) 에서 빛이 각기 다른 두 축(수평, 수직)에서 굴절되며, 초점이 하나로 모이지 않고 원뿔 형태의 초점 범위를 형성한다는 것을 설명합니다.
난시 연구와 광학 발전에 중요한 이론적 토대를 제공하며, 오늘날 난시 교정 렌즈 설계에도 활용되고 있습니다.
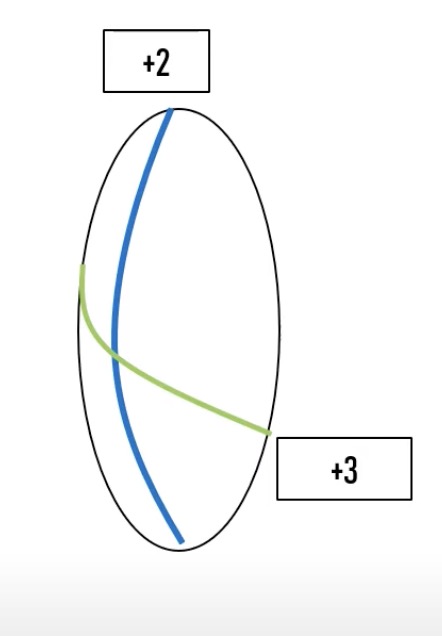
위와같이, 수직 축은 +2 만큼의 굴절력을 가졌지만, 수평축은 +3의 굴절력을 가진 난시렌즈(토릭렌즈)가 있다고 가정을 해봅시다.
즉, 수평쪽이 더 볼록한 렌즈라고 생각을 하시면 됩니다.
(난시렌즈에 대한 개념은 이전 포스팅을 참고 바랍니다)
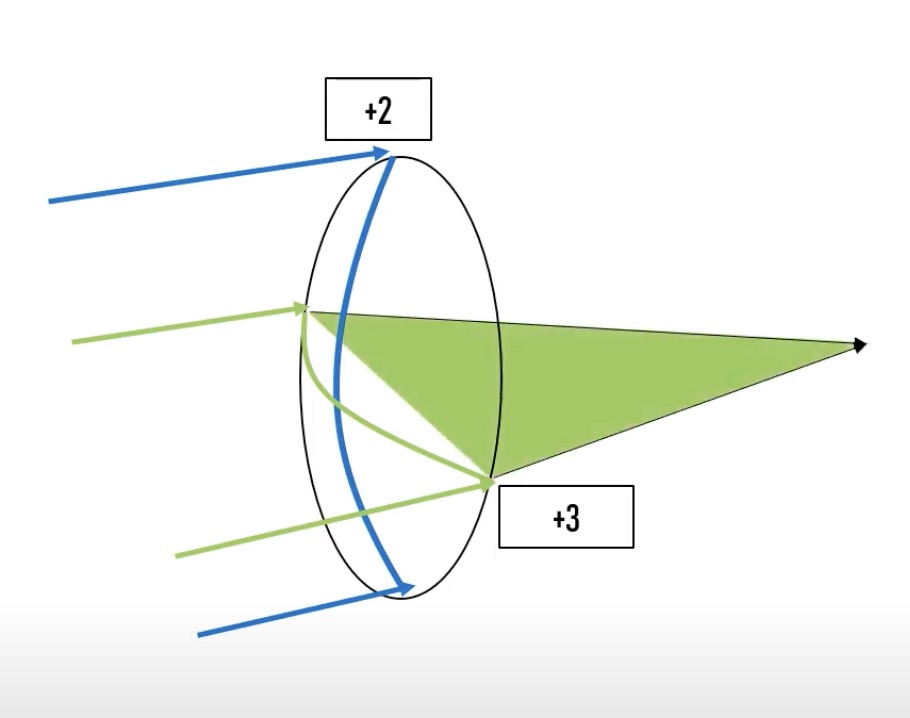
따라서 수평으로 들어오는 빛을 많이 모아줄 수 있게 되겠죠?
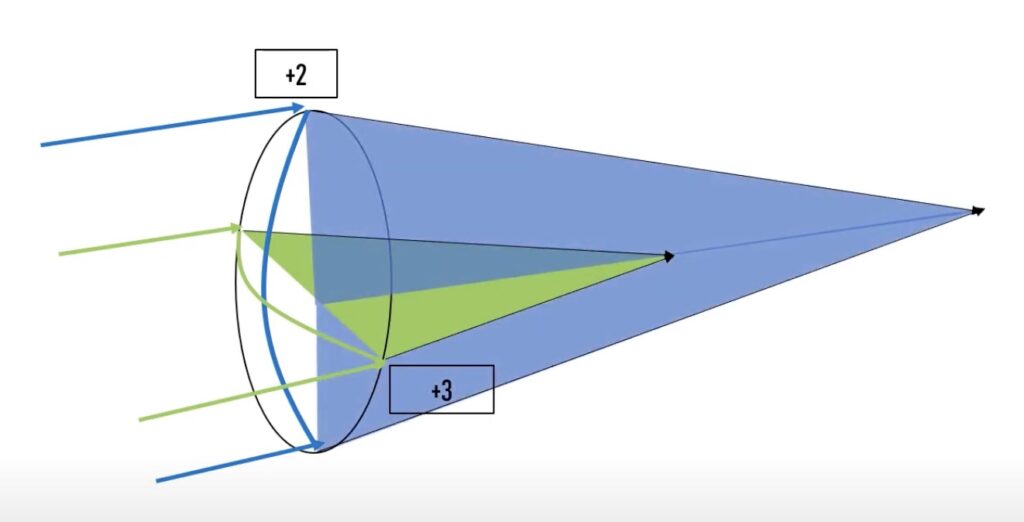
반면에 수직으로 들어오는 빛은 덜 모아지기 때문에 위 그림과 같이 초점이 더 뒤에 떨어지게 됩니다.
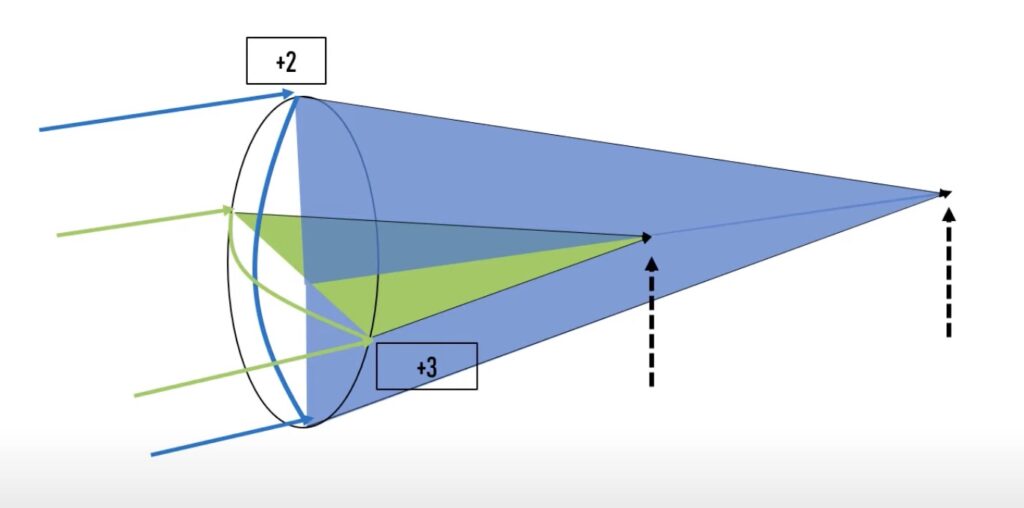
위 그림과 같이 수평축과 수직축의 빛이 가지는 초점이 다르게 형성이 됩니다.
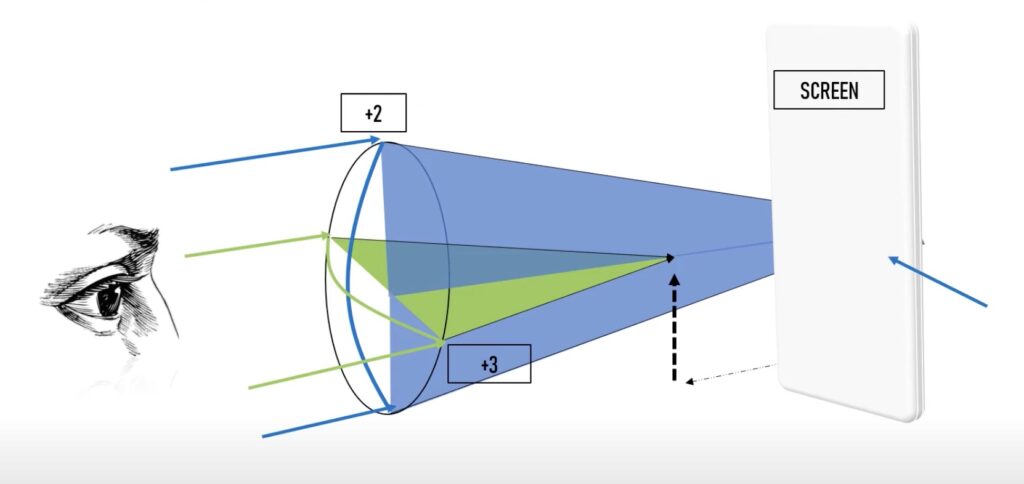
이러한 상황에서 빛의 경로에 스크린을 대어 스크린에 비춰진 빛 모양이 어떻게 변하는지 스크린을 다양하게 위치시켜보며 살펴봅시다.
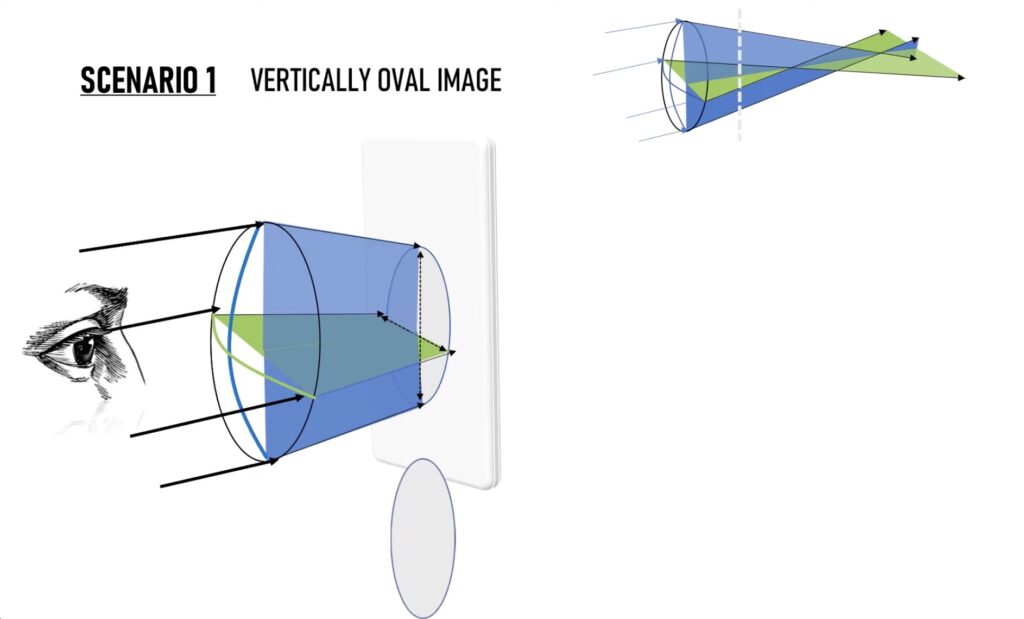
먼저, 두 초점보다 모두 앞에 스크린을 대면 위 그림과 같이 수직으로 생긴 타원형의 모양이 비춰짐을 알 수 있습니다.
여기서 스크린을 더 뒤로 이동을 해보겠습니다.
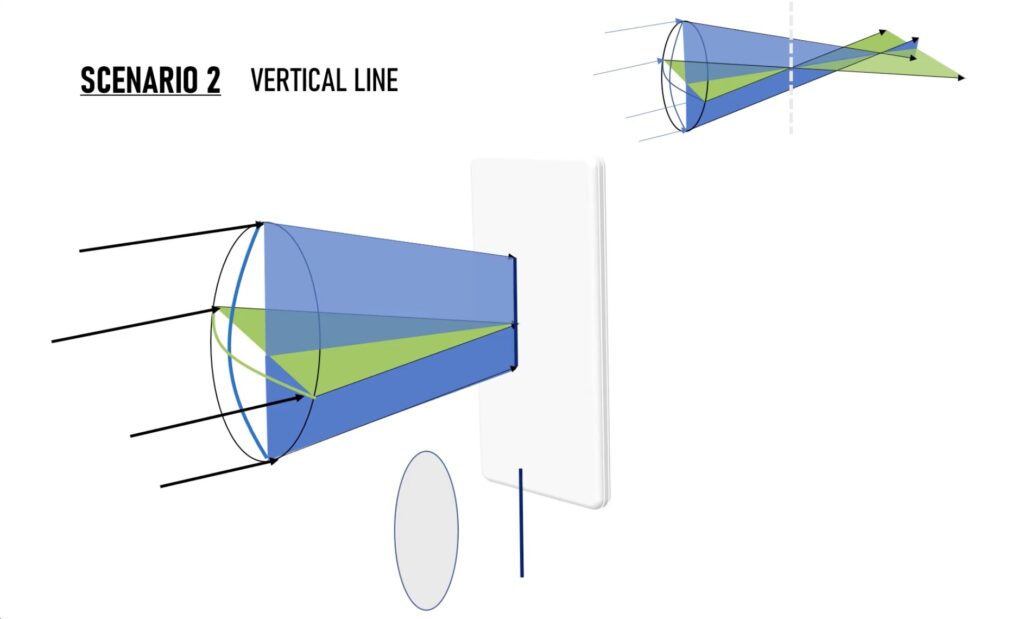
더 이동하여 수평축에 의해 만들어진 첫 번째 초점까지 스크린을 이동시켰습니다.
수평에서 들어온 빛은 완전히 수렴되기 때문에, 스크린에 비춰진 그림은 위와 같이 수직의 선 형태가 될 것입니다.
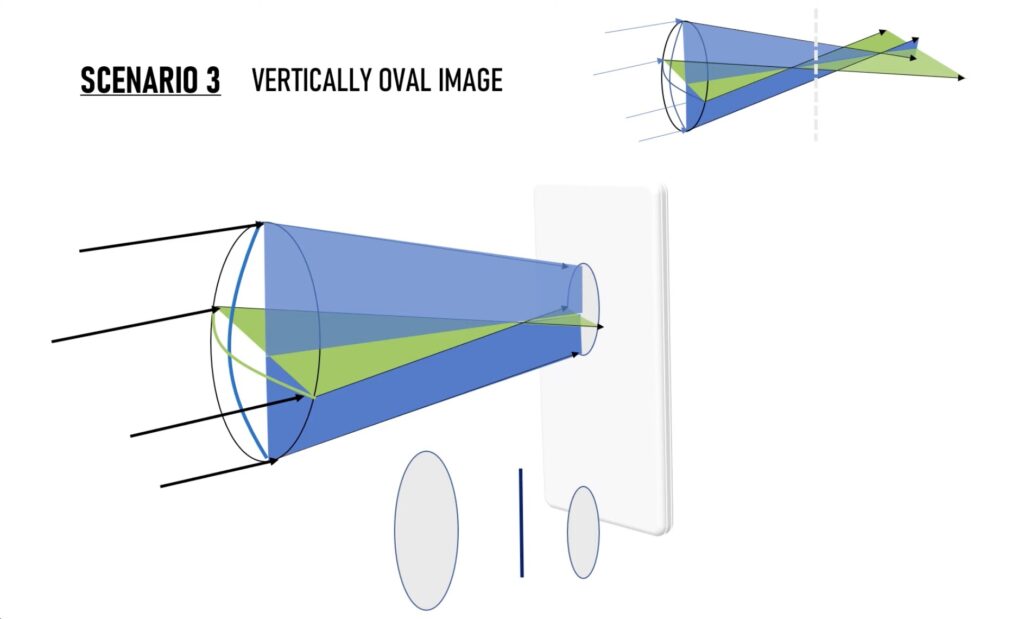
첫 초점을 지나 좀 더 뒤로 이동을 해보겠습니다.
수평축의 빛은 초점까지 모였다가 다시 퍼지기 때문에, 다시 타원형태의 모양을 가지게 됩니다.
하지만 수직축의 빛도 계속 수렴을 하기 때문에 위아래로 더 점점 더 작아지게 되어 작은 타원이 보이겠네요.
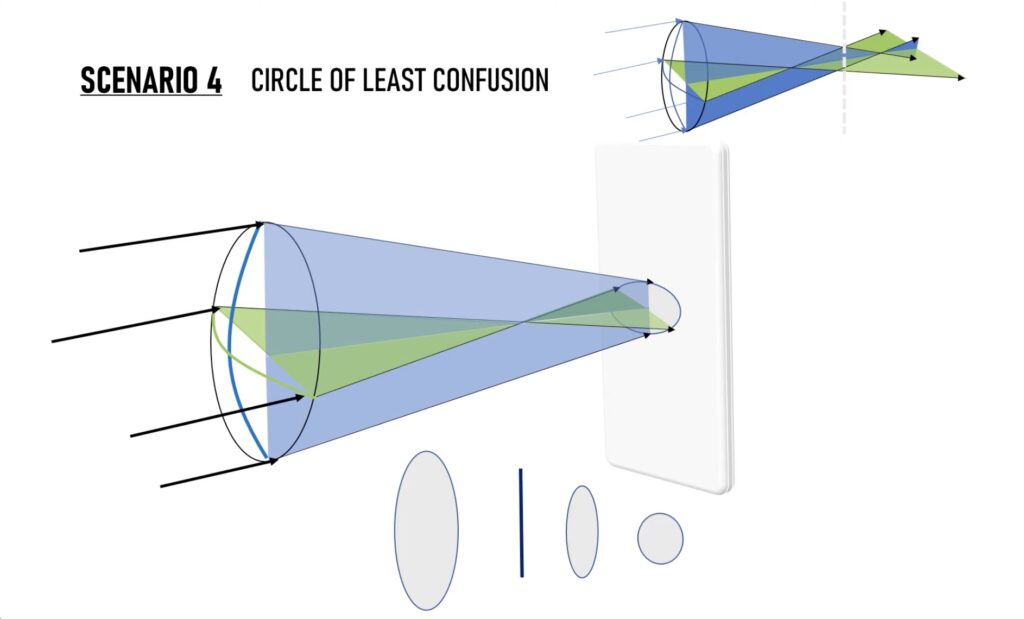
좀 더 뒤로가면서 수직축과 수평축이 딱 같은 만큼 수렴 혹은 발산된 지점이 있습니다.
이 지점에서는 정 원 형태의 모양이 보이는데, 이를 “최소 착란원(circle of least confusion)”이라고 합니다.
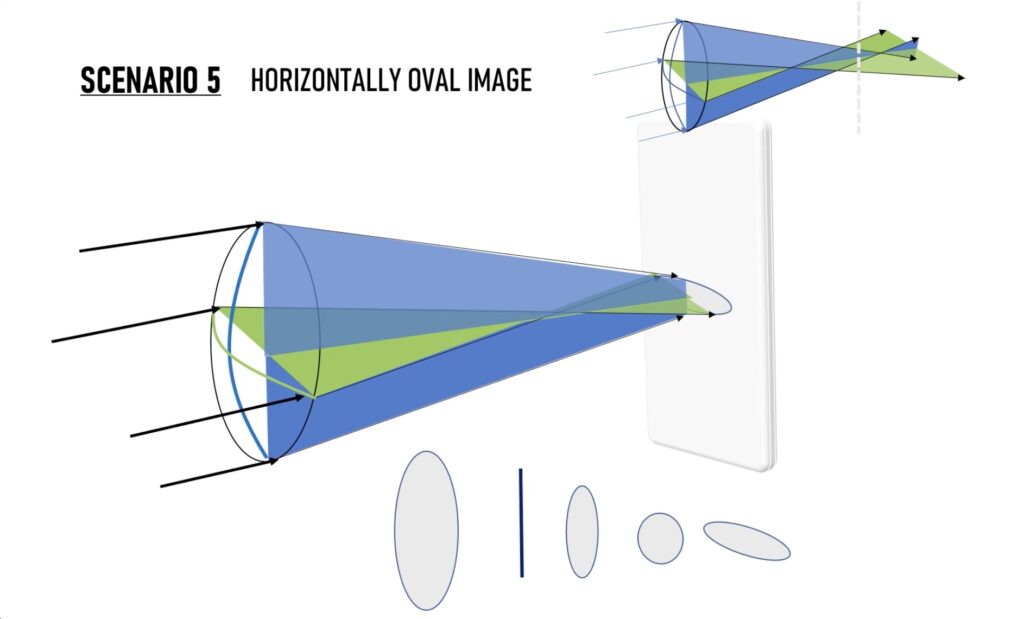
더 나아가 수직축이 수평축보다 좁아지게 되면 위와 같이 옆으로 퍼진 타원형이 보이고
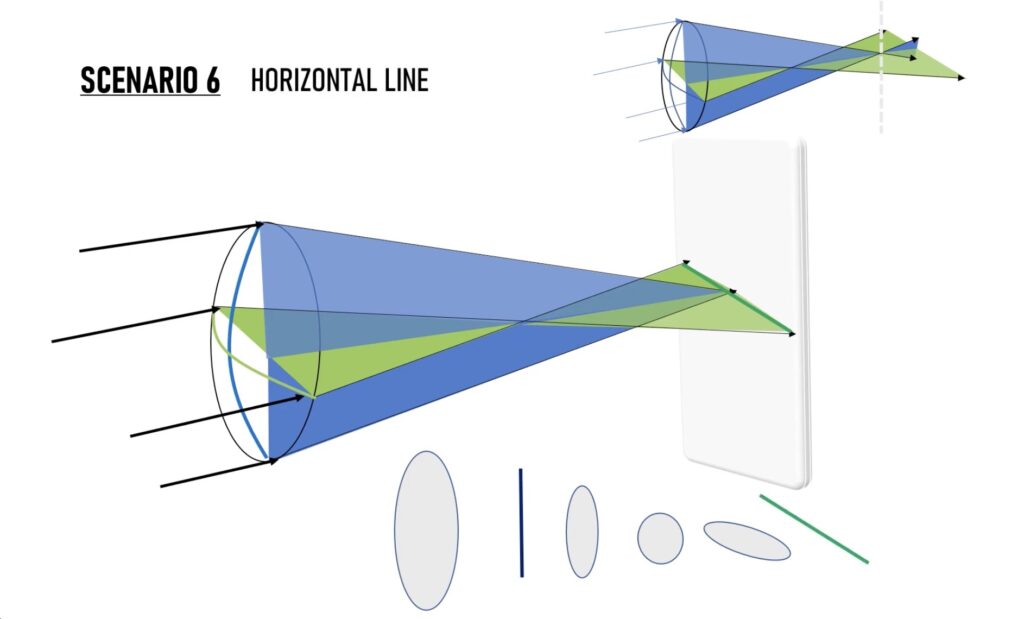
마침네 수직축의 초점에 다다르면 수직축은 완전히 수렴되어 위와 같은 수평 선의 형태로 스크린에 비춰질 것입니다.
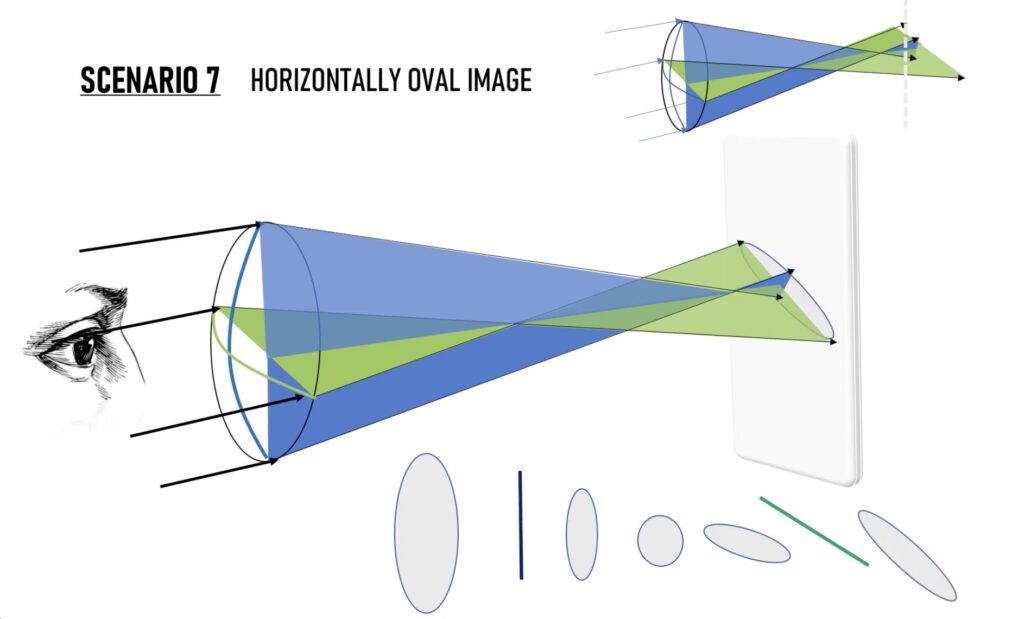
수직축의 초점도 넘어 뒤로 가면, 수직축도 다시 발산하기 때문에 위와 같이 수평의 타원형으로 보이기 시작합니다.
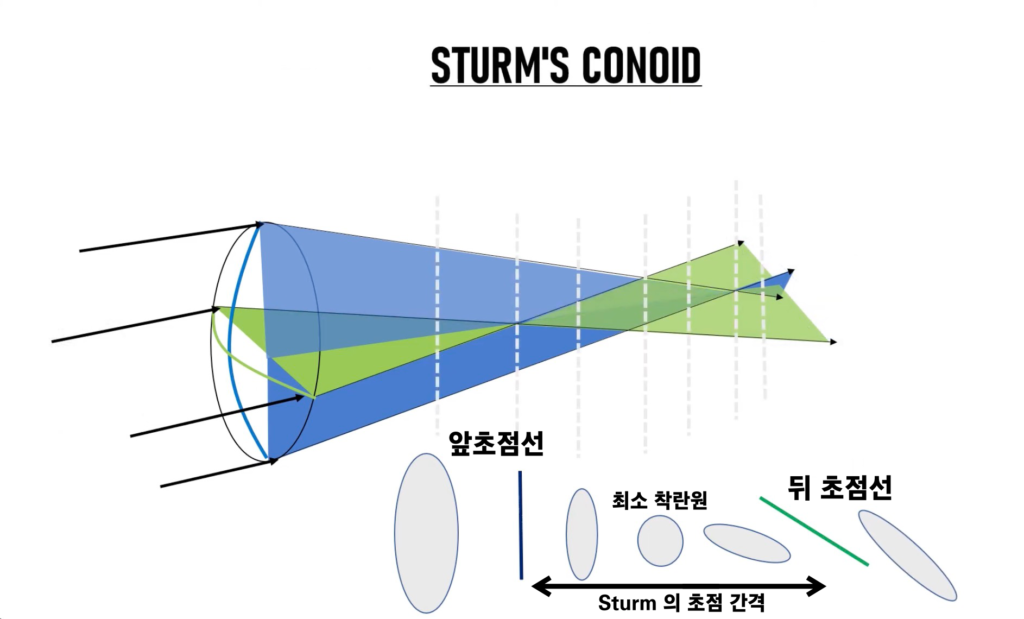
이것이 Sturm of conoid의 기본 개념이 되겠습니다.
난시의 여러 형태
이제 위의 이해를 바탕으로 여러 예시를 보겠습니다.
정시
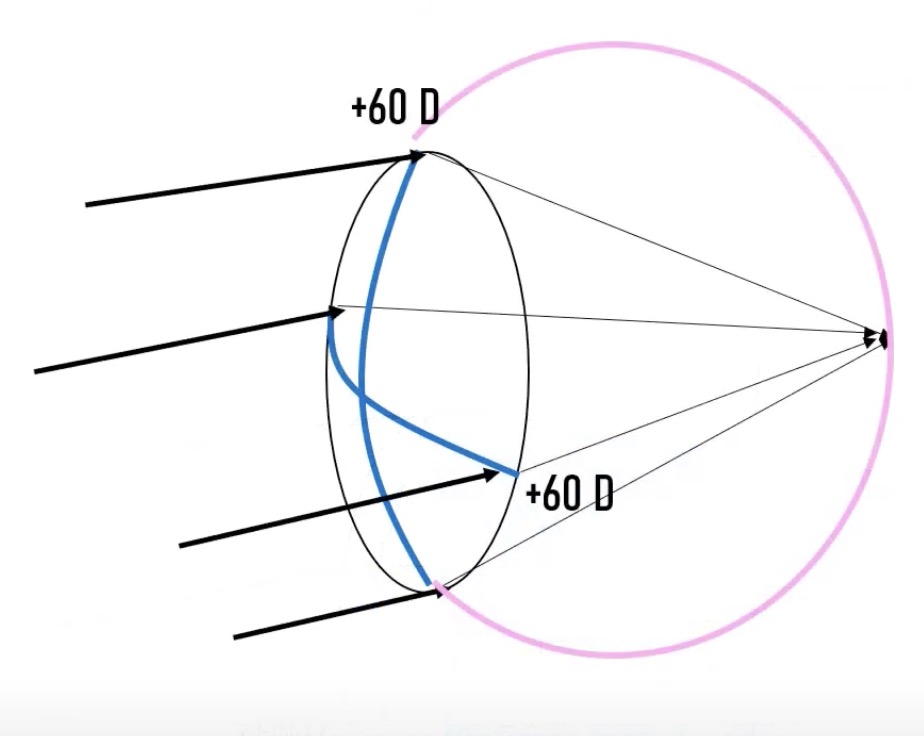
우리 각막이 대략 60 디옵터 정도의 굴절력(파워)를 가진 눈을 정시(emmetropia)라고 가정합시다.
정시이기 때문에 위와 같이 망막에 정확히 초점이 떨어집니다.
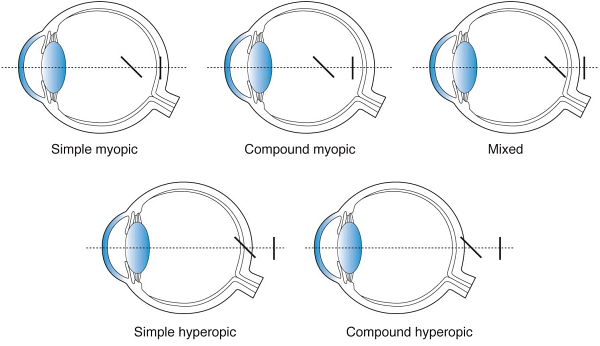
단순 원시
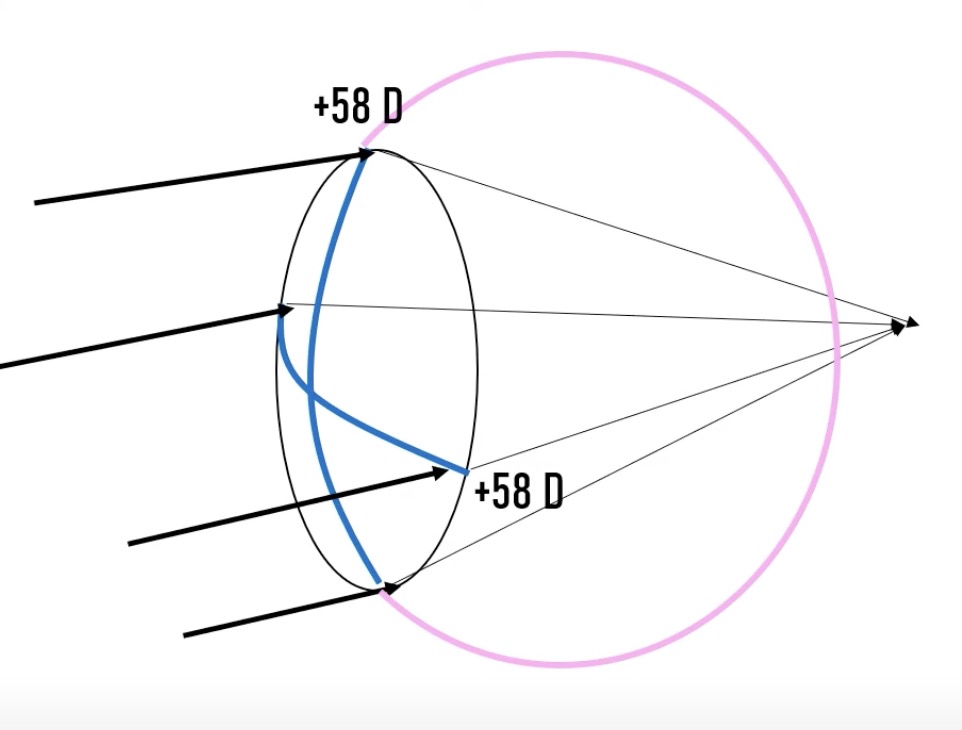
하지만 위와 같이 각막 파워가 58로 정시에 비해 2D 모자란 경우를 상상해 봅니다.
2D만큼 덜 꺾어주기 때문에 빛이 망막 뒤에 초점이 잡히게 됩니다.
이를 단순 원시(simple hyperopia)라고 합니다.
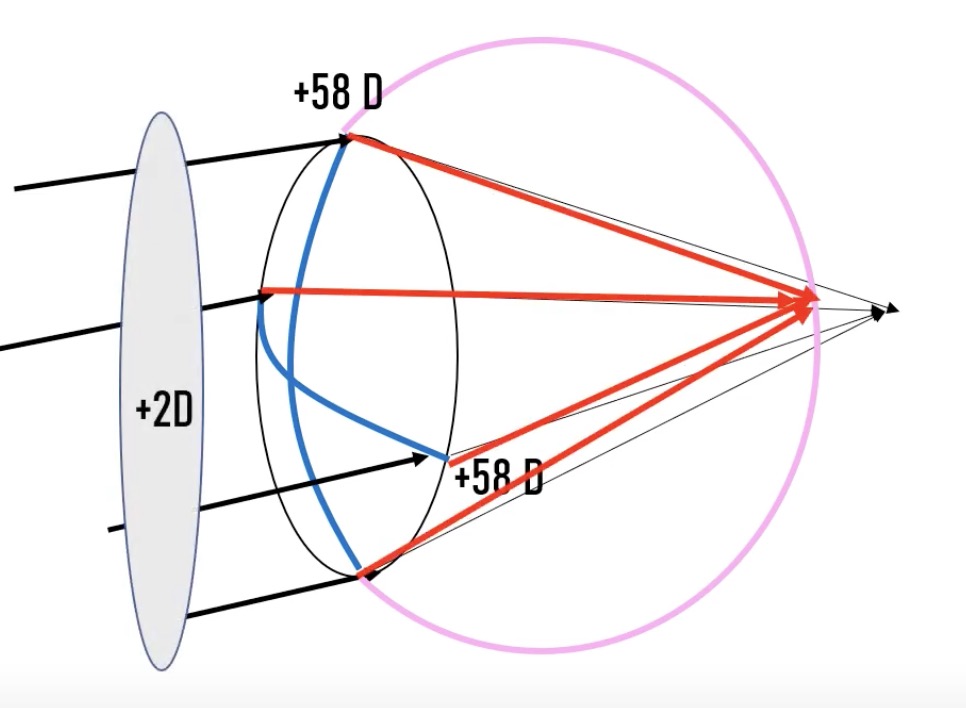
이런 눈은 눈 앞에 2D 파워를 가진 볼록렌즈를 대어주면 간단하게 교정이 가능합니다.
복합 근시성 난시
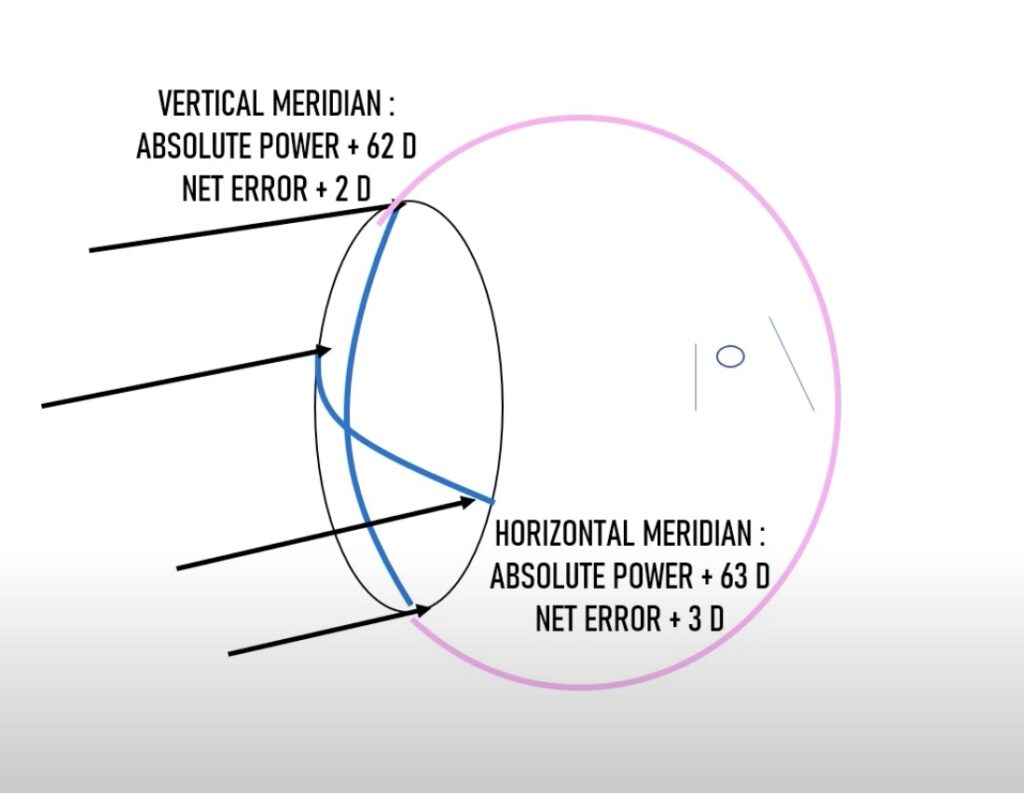
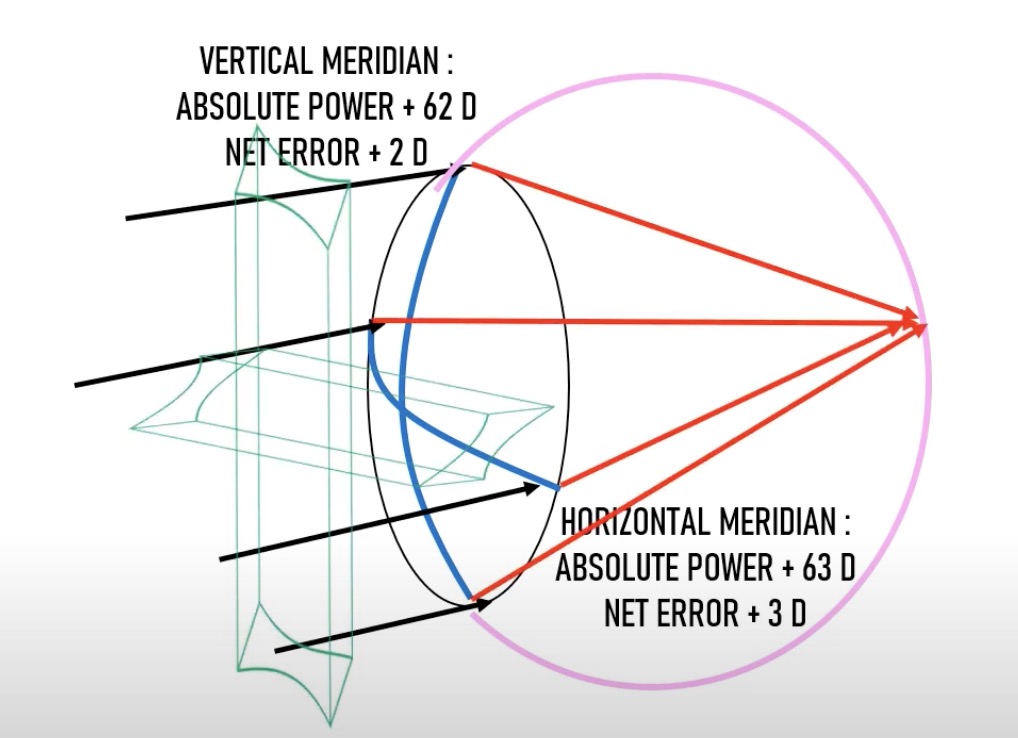
자, 이제 위의 그림처럼 수평축은 63D. 수직축은 62D의 가파른 각막이 있다고 가정을 해 봅시다.
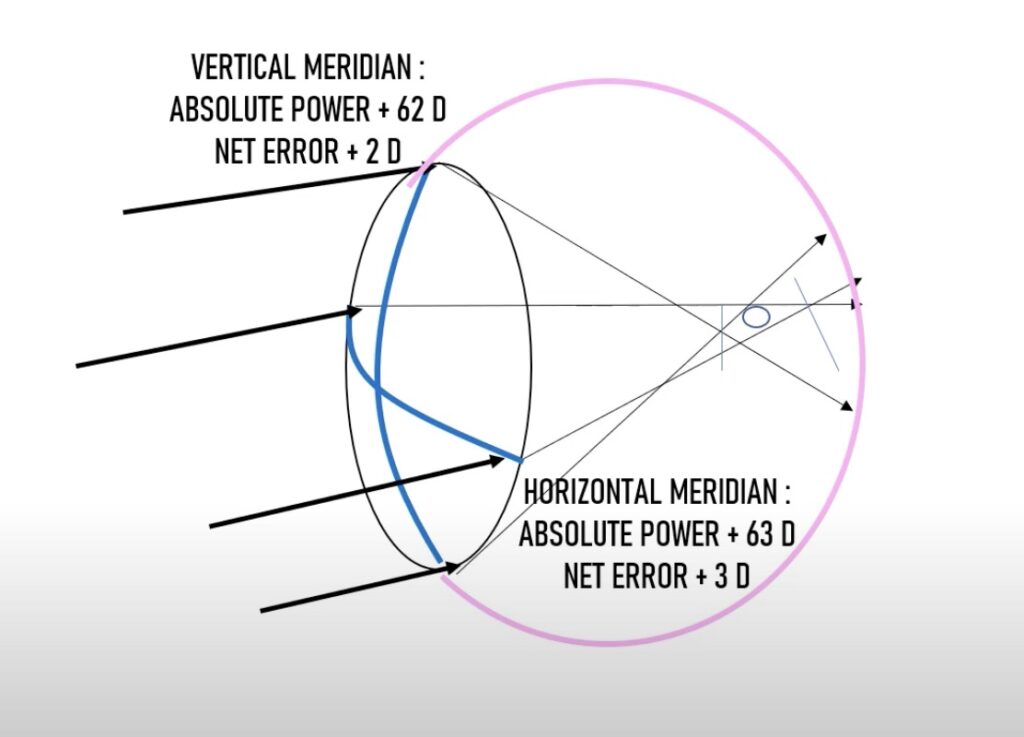
위 그림처럼 두 초점선은 서로 다르게 형성되며 모두 망막 앞쪽에 생기게 됩니다.
이를 복합 근시성 난시라고 부릅니다.
위 눈에서 초점을 망막 한 곳에 맞추려면 어떻게 해야 할까요?
-2D 의 원주렌즈를 180도 방향으로 놓고, -3D 원주렌즈를 90도로 위치시키면 두 축에서 나오는 빛을 망막의 한 점으로 모을 수 있습니다.
하지만 이렇게 원주렌즈만으로 처방을 할 수는 없어 결국
-2D 구면렌즈에 -1D 원주렌즈 90도 방향의 안경 처방이 됩니다. (-2.0D sph -1.0D @ 90)
이처럼, 축이 서로 90도 방향을 이루는 “규칙성 난시”에서 sturm of conoid를 하나의 점으로 합치려면 구면+원주렌즈(난시렌즈) 를 통해서만 가능합니다.
(불규칙 난시는 이런 개념이 통하지 않습니다)
구면대응치
만약 위 경우를 원주렌즈 없이 교정을 해야 한다면 어떻게 해야 할까요?
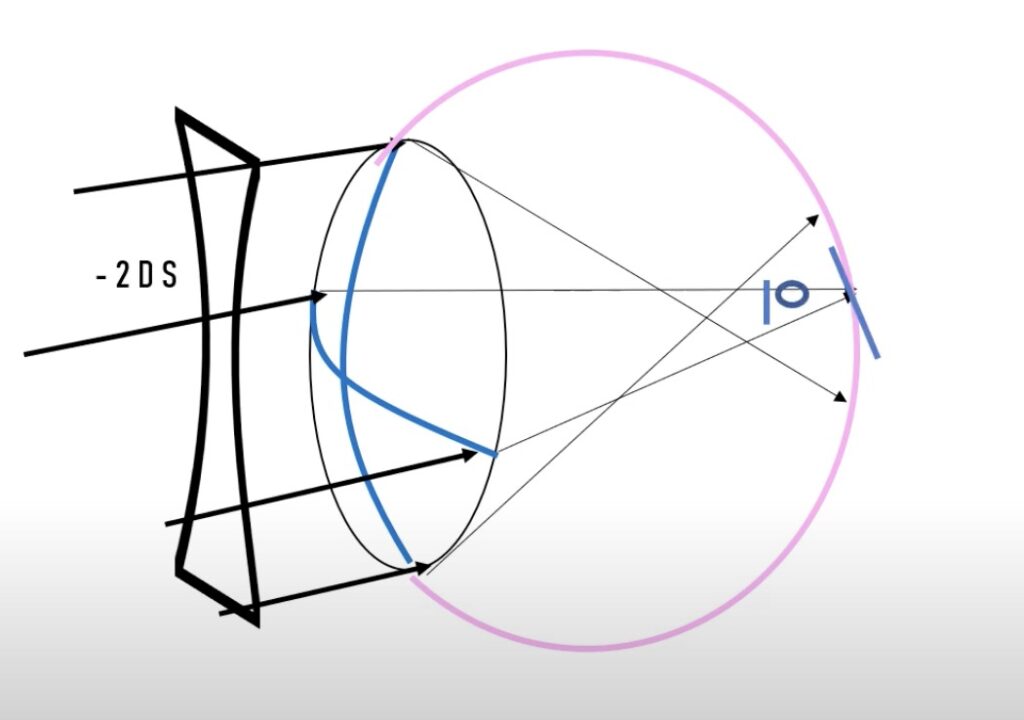
만약 -2D 의 구면렌즈로만 교정을 한다면, 위와같이 뒤 초점은 망막에 떨어뜨릴 수 있겠지만 여전히 옆으로 퍼져보이는 이미지를 얻게 됩니다.
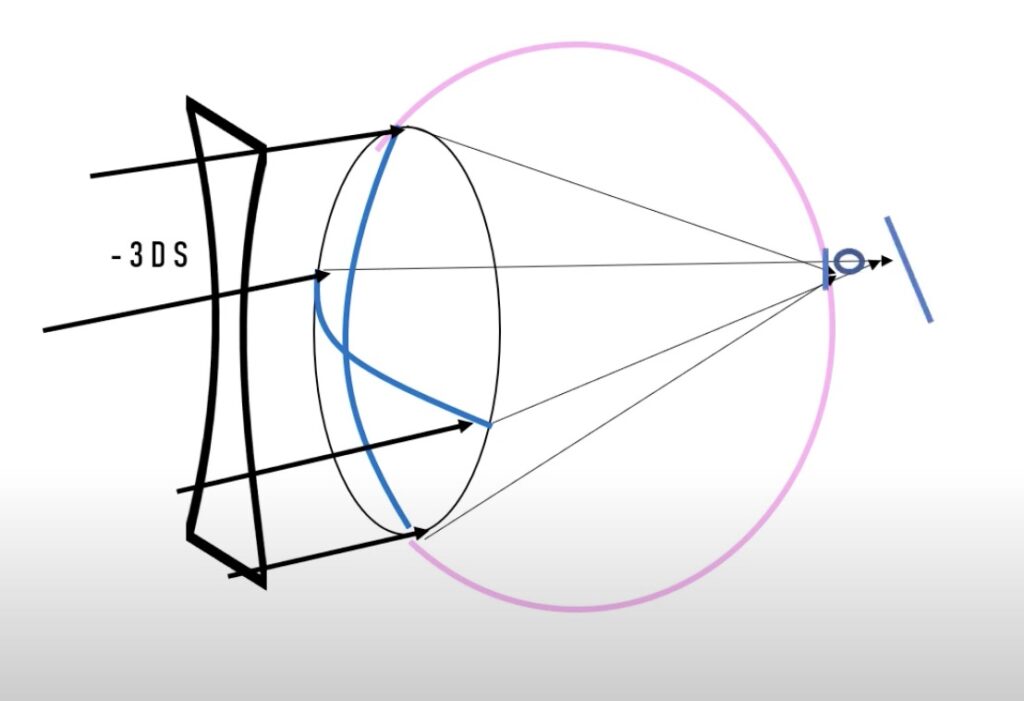
-3D의 구면렌즈를 사용한 경우는 앞초점을 망막에 떨어뜨릴 수 있지만 여전히 위아래로 퍼져보이는 이미지가 생깁니다.
앞서 배운 최소착란원(circle of least confusion)은 sturm of conoid에서 그나마 점에 가까운 이미지를 제공합니다.
따라서 원주렌즈를 통한 교정이 없다면, 이 최소착란원의 위치가 최선의 선택이 됩니다.
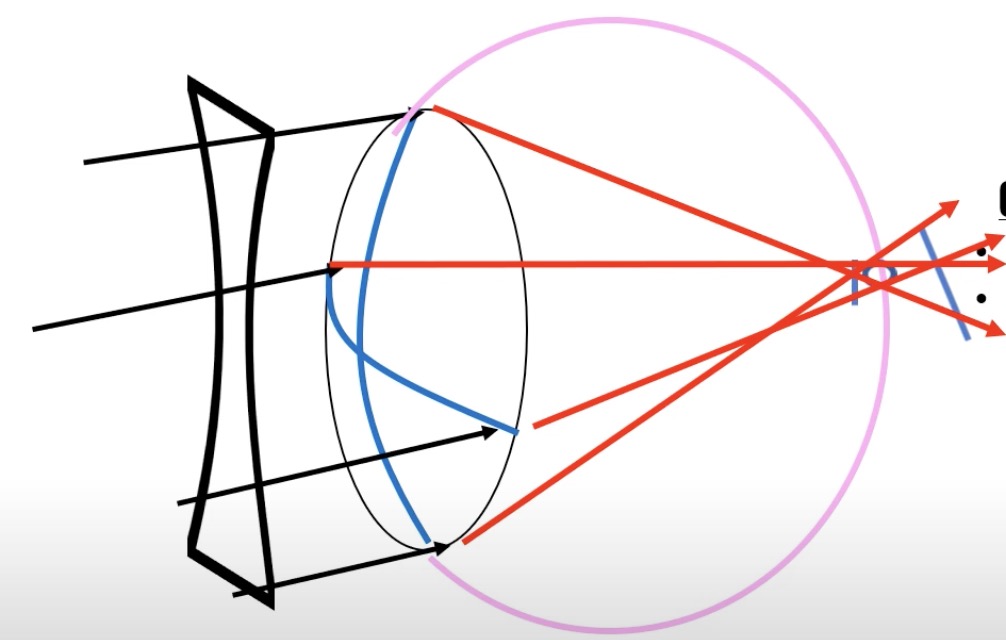
이러한 최소착란원을 망막에 떨어뜨릴 수 있는 도수를 구면대응치(spherical equivalent =S.E)라고 합니다.
이 구면대응치를 계산하는 방법은 간단합니다.
S.E = 구면값 + 1/2 원주값(축은 무시)
따라서, 이 환자의 원래 안경처방 값인 -2.0D sph -1.0D @ 90 에서 계산을 해 보면
(-2) + 1/2(-1) =-2.5
즉 -2.5 가 구면대응치가 되겠습니다.
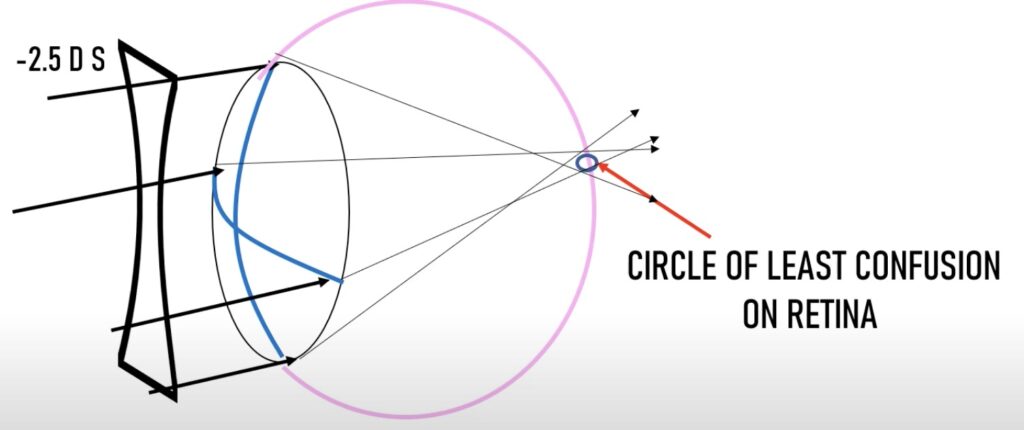
그림과 같이 -2.5 D 의 구면렌즈를 통해 최소착란원을 망막에 맞출 수 있는 것이죠.
마무리
이렇게 난시란 무엇인지 기본 개념에 대해서 확실하게 정리를 해 보았습니다.
이런 기본 이해가 있어야 다음 이해가 가능하답니다.
다음 시간에는
각막난시, 굴절난시 둘 차이는 무엇이며 각각 어떤 의미가 있는지에 대해 알아보도록 하겠습니다.
백내장, 굴절수술에 있어 핵심인 내용입니다.
긴 글 읽어주셔서 감사합니다.
질문은 커뮤니티를 이용 바랍니다.